You're Diversifying Wrong

When can diversification be a bad thing?

“Diversification is the only free lunch” - Harry Markowitz

The three steps to diversification

Imagine a casino with a single dice game:

• If you roll a 1, you lose 27.5%

• If you roll a 2, 3, 4 , or 5 you gain 2%

• If you roll a 6, you gain 27.5%

You get to choose how much you bet, and there are two tables running at the same time. You bring some buddies and decide to split your money across the two tables, so you can diversify your bets— after all, it is the “only free lunch” in investing, according to Markowitz.

“Diversification is for idiots” - Warren Buffet (paraphrasing, of course)

Let’s step out of the Casino for a second.

Most people don’t think about diversification past the platitudes. I’ve had thousands of conversations on risk management in the past few years, and haven’t heard any real original thinking on the topic in that time. If the topic is raised to a efficient market disciple, they’ll quote Markowitz “diversification is the only free lunch”, if the manager goes to Omaha each year they’ll quote Buffet “diversification is a protection against ignorance”. If the manager has really gone out of their way to read about diversification, they will bring up Ray Dalio’s famous chart on the number of securities held vs. the reduction in volatility.

“Diversification = Risk Parity” - Ray Dalio (one again, paraphrasing)

The issue I have with diversification is that it conflates multiple steps. When you sit down at two separate tables and diversify your bets, you’re actually doing three different things.

First, you’re lowering your allocation to any single bet. As we’ve discussed before lowering your allocation to any given bet can actually increase your long term rate of compounding.¹ Second, after that lower sizing has occurred, you are allocating excess cash to a second bet. Lastly, you’re rebalancing between each game.

This happens in the real world as well. A stock picker will lower their allocation to $GOOG from 40% to 20% so they can make room for $AAPL, and think of the entire transaction as diversifying. Similarly, when quants go to prove the benefits of diversification, they bundle all three of these things and then prove that together the create a portfolio benefit.

Diversification’s decomposition

Let’s de-conflate our game, and go step by step to understand where this “free lunch” occurs.

Step 1: Kelly

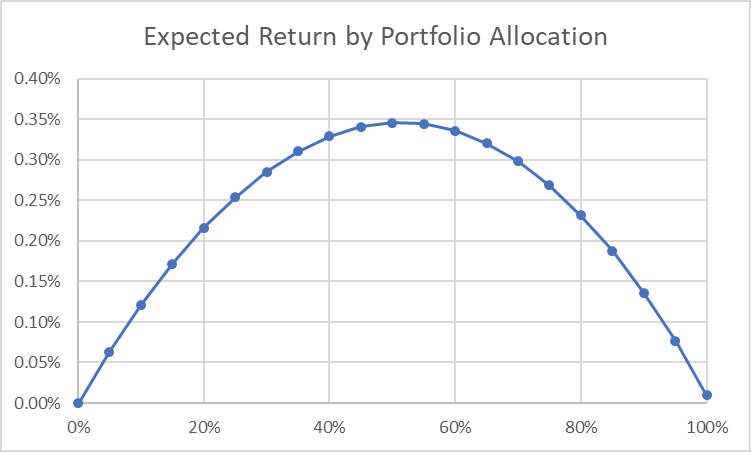
As we’ve discussed before, lowering an allocation to any specific bet can actually maximize a wager’s CAGR. For this specific bet, a 100% allocation yields a long term CAGR of ~0.01%, while the optimal allocation of c. 50% yields a long term CAGR of ~0.35%.

Yes, I made the numbers work such that 50% is an optimal allocation here.

Step 2: Cash optimization

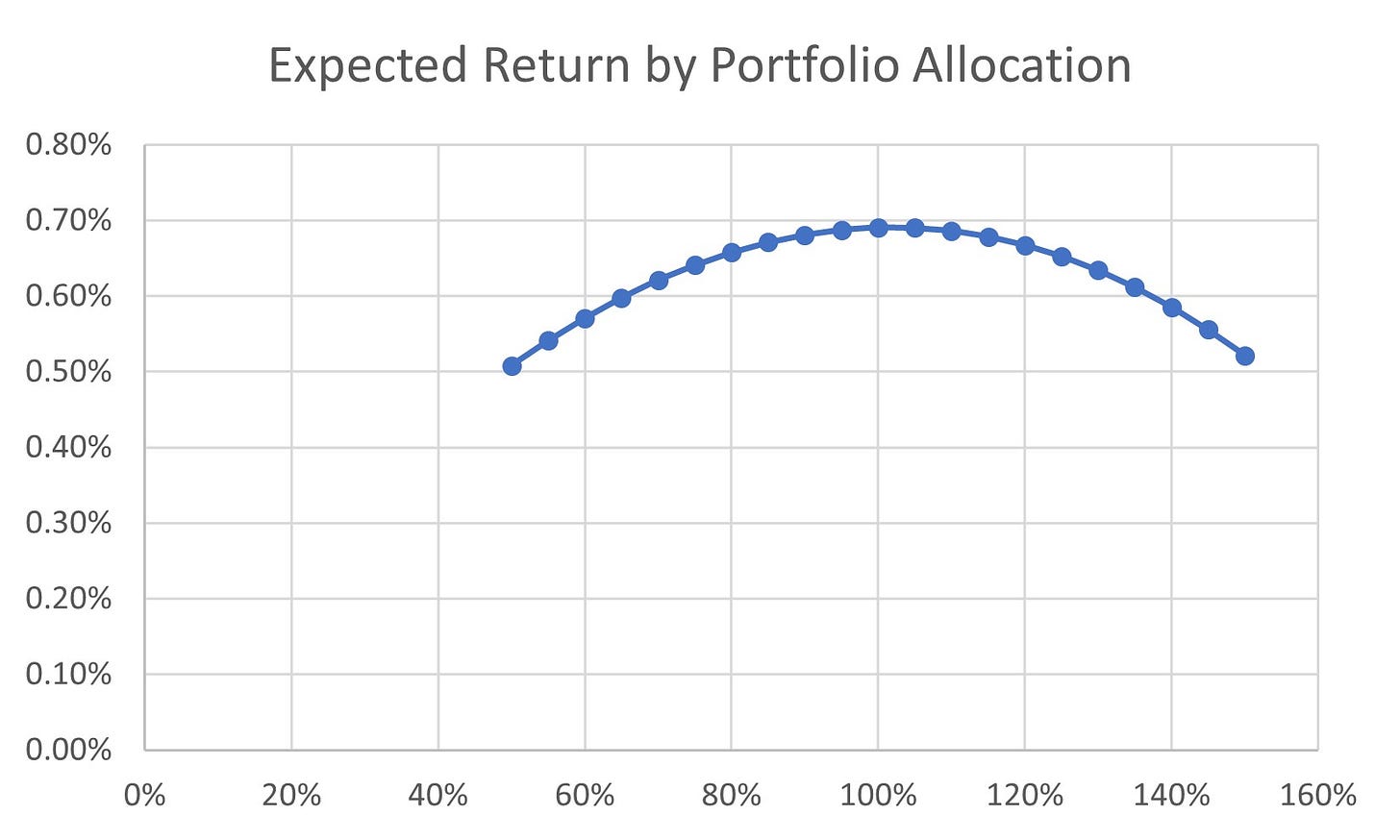
If we know that the optimized allocation of our capital in this game is 50%, that leaves 50% of our capital in cash at any given time. That is obviously less than optimal. So the next step of diversification at the casino is to give our buddies the other 50% of our cash, and have them sit down at the other table. This immediately increases our expected compounding rate on the first hand. In fact, it doubles the expected return we saw previously. So now our expected long term CAGR as gone from 0.35% to 0.70%

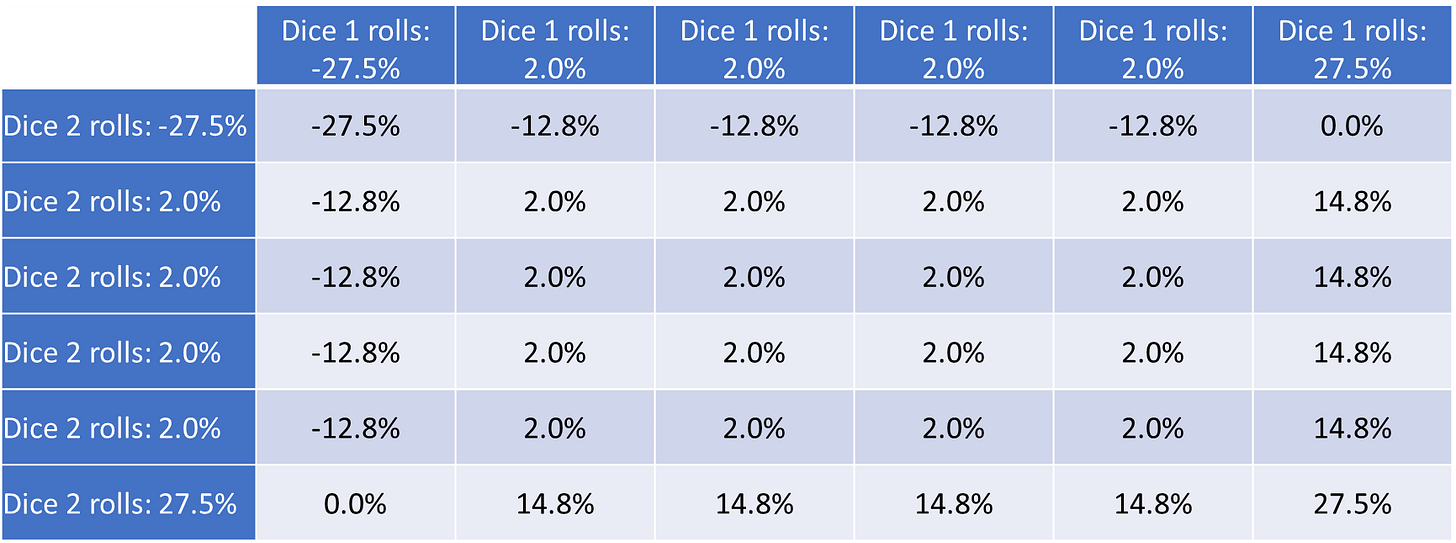
Another way to think about this, is that by running two games at once, we’re actually just changing the rules of our game. Instead of rolling a 6 sided die, now we’re rolling a 36 sided die, where each box below represents a 1/36 chance of occurring:

If we treat this as a brand new game, and calculate it’s optimal allocation the math ties out nicely, and we find the optimal allocation is at 100%, with an expected long term CAGR of c. 0.70%.

Step 3: Rebalancing

The last thing we need to do occurs after the first roll— we need to rebalance our capital between the two tables. The impact here is a little bit trickier to quantify for one simple reason: the first two steps already assume rebalancing.

If we don’t rebalance we’re basically skipping step one. I.e., if we take two separate piles of cash, and we don’t rebalance between them, what you’re running is two separate portfolios, both at a 100% allocation— the returns for each will be 0.01%.

Therefore, as soon as we decide that we want to follow Kelly, we have implicitly decided that we want to rebalance.

Bringing it all together

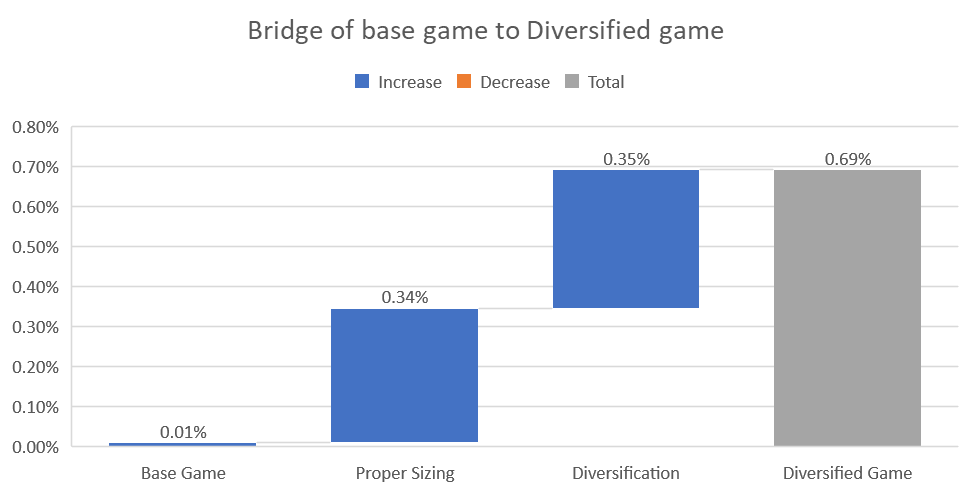
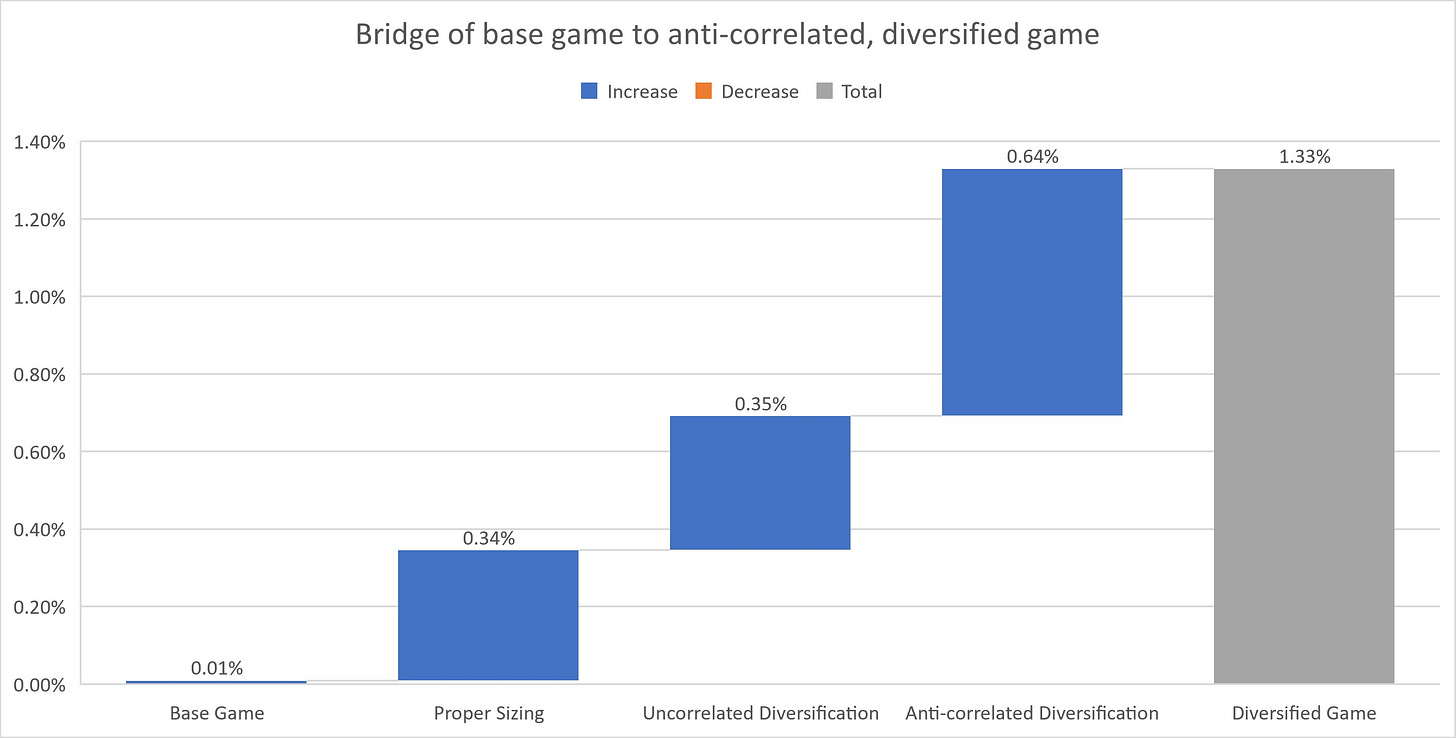
If I were writing a paper about diversification’s benefits here, what I could show is that a single security portfolio has an expected CAGR of c. 0.01%, while a diversified and rebalanced portfolio has a CAGR of c. 0.70%. Oh the miracles of diversification— the only true free lunch!

But in reality, an enormous portion of that benefit doesn’t come from diversification at all— it comes from proper bet sizing.

But this is only for an uncorrelated game— what happens when we choose games that are positively or negatively correlated?

The impact of correlation

Positive correlation

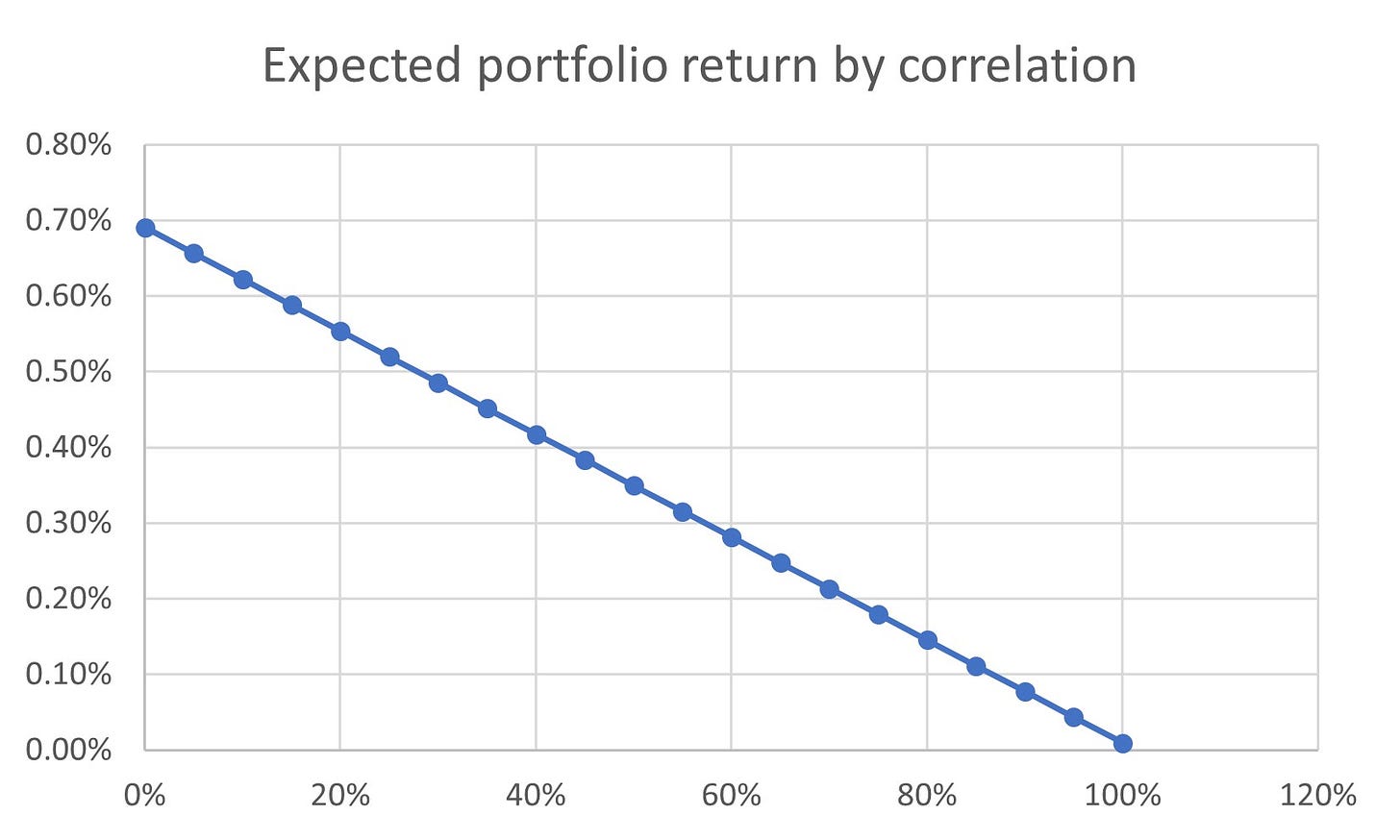
In the stock market, most securities move together. The world isn’t as clean as a dice game, and it’s generally difficult to find uncorrelated returns. So how does the waterfall chart change as we increase the correlation of securities in the portfolio?

One way to think about this directionally is to take the extreme. Let’s consider what would happen if the bets were 100% positively correlated. That scenario would be effectively the same as bringing our allocation of the starting bet back to 100%. For example, if we rolled a 1 on one table, we would lose 27.5% on both bets, which comprises 100% of our allocations— effectively the same as if we had just made a single bet. We know the long term compounding rate for this allocation level— it’s 0.01%.

So if we know that a 100% positive correlation creates a 0.01% CAGR, and a 0% correlation creates a 0.70% CAGR, then we know that all other positive correlations will fall somewhere in between. So at what point does the benefit of diversification stop being beneficial?

This math is game-by-game specific, but in our fictional casino the correlation at which the benefit of further cash optimization is outweighed by the harm of incrementally concentrated risk is about at ~50%.²

Negative correlation

So if positive correlation is a bad thing for the portfolio, negative correlation is obviously a good thing.

Let’s once again start by taking the extreme here— in a world with two tables in the casino that are 100% anti-correlated, we can actually simplify the whole dynamic back into a single game:

• If we roll a 1 or a 6 at the first table, we know we will roll a 6 or a 1 at the other. our losses net out with our winnings, and so we make net 0%

• If we roll a 2, 3, 4, or 5 at one table, we know we will also roll that at the other table. Therefore, we make 2%

At a 100% allocation (a.k.a. 50% at each table) this gives us an expected CAGR of 1.33%— almost DOUBLE our previous c. 0.70%. This shows the massive importance of correlations in diversification. While too high of an allocation to a positively correlated asset can actually hurt returns, you can 1.9x your CAGR by simply finding a positive EV, anti correlated assets:

Impact for a fundamental PM

So with this quick little exercise, I think there are a few simple takeaways:

Many people misattribute the benefits of proper sizing to diversification

If we go back to the original waterfall chart— proper position sizing was ~50% of the benefit of diversification. While the math isn’t as clean in the real world (and differs wager to wager) it does show that thinking about portfolio construction bottom up can often compliment the top down views. And as the beta and industry exposures are in the right range, diversification within equity markets may not be as important as people believe.

Diversification can harm you if you diversify into positively correlated risks

For stock pickers, the vast majority of returns are going to be driven by the equity risk premia. When you “diversify” away from $GOOG and into $AAPL, you’ve removed and then added back the same sensitivity to economic growth and multiple compression/expansion that will largely define the returns for both companies. In other words, correlations within the equity market are high enough that the diversification benefit you get from picking multiple stocks is more about reduction of tracking error than it is increasing of expected long term CAGR.

The most important portfolio construction decision an equity PMs needs to make is what the proper level of equity premia risk they should be taking. When you add or reduce allocations, the beta of each position differs. While over the long term the optimal portfolio beta is ~1.5x, you can see some growth managers looking at high beta names, and running a portfolio at 2x+. For those managers, diversification isn’t going to help— what they need is to better tune their beta allocation decisions.

This is also where Dalio picks up— his point has always been that even if an allocator’s dollars are diversified, the majority of risk is concentrated equity risk premia. He advocates finding uncorrelated risk premia by looking away from domestic equity markets towards emerging markets, domestic and sovereign yields etc.

The benefits of diversification comes from negative correlations

My old boss and I used to talk about the “diversification benefit” of a strategy— measured as the impact to long term compounding rate of an asset. Sometimes this quantification could be strongly positive, while their actual real returns were negative.

This is true with an incredible number of investments— puts, gold, CTAs, insurance. Many PMs are quick to dismiss an investment as being negative EV, but miss that portfolios can still benefit from these securities as long as the correlations are right.

1. As an aside, Aaron Brown’s chapter “When Harry met Kelly” in Red Blooded Risk Management was the first thing I’ve ever read that introduced this idea of proper sizing being an enormous part of the incremental benefit of diversification.

2. The math works out like this because we made the original game be Kelly-maximized at 50%. Because of that, the combined uncorrelated portfolio is maximized at 100%, and as the benefit is linear, the correlation at which the benefit of diversification outweighs the single game is also at 50% (1/5 the 100% allocation)